티칭백과란?
교과별 특성을 고려한 맞춤형 콘텐츠로서, 스마트한 수업과 자기주도학습을 지원하는 온라인 백과사전 서비스입니다.
- 지원 서비스
- - 주제별 맞춤 지식 공유
- - 다양한 스마트 기기 지원
- - 멀티미디어 자료 제공
거듭제곱 power
\(a^2,~ a^3,~ a^4,~ \cdots\)을 통틀어 \(a\)의 거듭제곱이라고 한다.
같은 수를 여러 번 반복하여 곱하는 것을 식으로 나타내면 너무 길어져 불편하므로 곱하는 수의 오른쪽 위에 곱하는 수의 개수를 써서 간단히 나타낸다.
예를 들어 \(2 \times 2=2^2,~ 2 \times 2 \times 2=2^3,~ 2 \times 2\times 2 \times 2=2^4,~ \cdots\)으로 나타내고 각각 \(2\)의 제곱, \(2\)의 세제곱, \(2\)의 네제곱, \(\cdots\)이라고 읽는다.
일반적으로 수 \(a\)에 대하여
$$a \times a=a^2,~ a \times a \times a=a^3,~ a \times a \times a \times a=a^4,~ \cdots$$
으로 나타내고, \(a^2,~ a^3,~ a^4,~ \cdots\)을 각각 \(a\)의 제곱, \(a\)의 세제곱, \(a\)의 네제곱, \(\cdots\)이라고 읽는다.
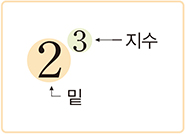
이때 \(a^2,~ a^3,~ a^4,~ \cdots\)을 통틀어 \(a\)의 거듭제곱이라고 하며 \(a\)를 밑, \(a\)를 곱한 개수를 나타내는 \(2,~ 3,~ 4,~ \cdots\)을 지수라고 한다.
- 관련교과서 : 금성 12쪽, 비상 14쪽, 두산(강) 17쪽, 천재(이) 19쪽, 미래엔 11쪽
\(3 \times 3 \times 3 \times 3 \times 3\)을 거듭제곱으로 나타내고, 밑과 지수를 말하여라.
더 알아보기
'거듭제곱'은 거듭하여 자신을 곱한다는 뜻이다.
예전에는 한자어인 자승(自乘), 삼승(三乘), 사승(四乘), \(\cdots\)을 사용하였으나 지금은 우리말 표현으로 바꾸어 사용한다.
\(a^1\)은 곱셈 연산을 한 것이 아니므로 거듭제곱이라고 부르기 어색하지만 그 표현 방법 때문에 \(a^1\)도 \(a\)의 거듭제곱으로 생각한다.
지식나눔
관련된 나의 지식을 등록하여 공유할 수 있습니다.
의견나눔
총 1개의 의견이 있습니다.
-
sor****** 2024-02-26
1. 제곱수 :어떤 자연수 를 두 번 곱해서 나오는 정수. 제곱수 형태를 수를 만들기 위해서는 인수분해를 먼저해줘야한다. 2. 약수의 개수가 3개인 자연수는? N=(소수)²










